#include <stdbool.h>#include <stddef.h>#include <stdint.h>#include <time.h>#include <string.h>#include "avl.h"#include "assert.h"#include "list.h"Go to the source code of this file.
Functions | |
| static int | avl_max (int x, int y) |
| static int | avl_min (int x, int y) |
| static struct avl_node * | avl_find_rec (struct avl_node *node, const void *key, avl_tree_comp comp, void *ptr, int *cmp_result) |
| static void | avl_insert_before (struct avl_tree *tree, struct avl_node *pos_node, struct avl_node *node) |
| static void | avl_insert_after (struct avl_tree *tree, struct avl_node *pos_node, struct avl_node *node) |
| static void | post_insert (struct avl_tree *tree, struct avl_node *node) |
| static void | avl_delete_worker (struct avl_tree *tree, struct avl_node *node) |
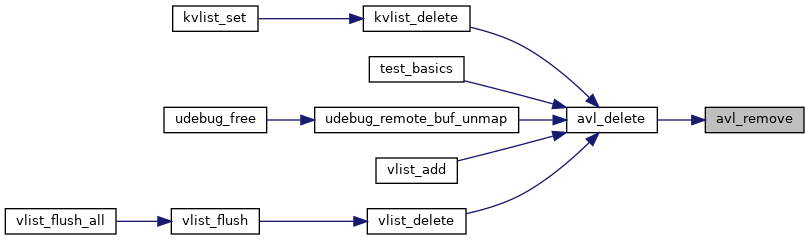
| static void | avl_remove (struct avl_tree *tree, struct avl_node *node) |
| void | avl_init (struct avl_tree *tree, avl_tree_comp comp, bool allow_dups, void *ptr) |
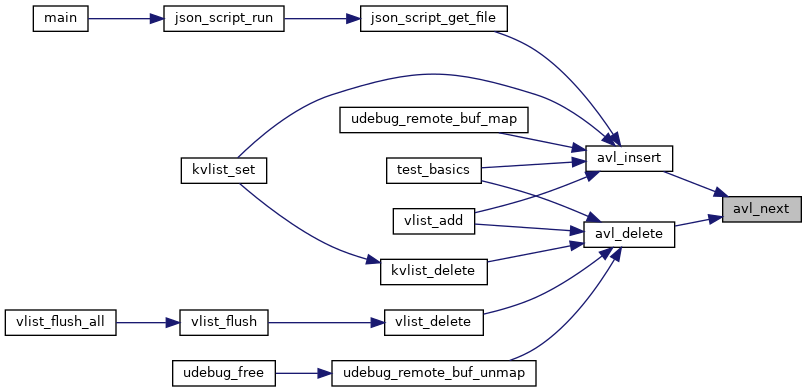
| static struct avl_node * | avl_next (struct avl_node *node) |
| struct avl_node * | avl_find (const struct avl_tree *tree, const void *key) |
| struct avl_node * | avl_find_lessequal (const struct avl_tree *tree, const void *key) |
| struct avl_node * | avl_find_greaterequal (const struct avl_tree *tree, const void *key) |
| int | avl_insert (struct avl_tree *tree, struct avl_node *new) |
| void | avl_delete (struct avl_tree *tree, struct avl_node *node) |
| static void | avl_rotate_right (struct avl_tree *tree, struct avl_node *node) |
| static void | avl_rotate_left (struct avl_tree *tree, struct avl_node *node) |
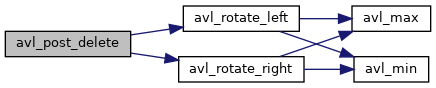
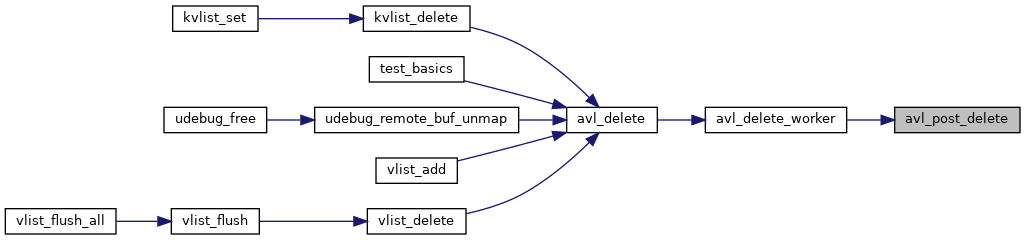
| static void | avl_post_delete (struct avl_tree *tree, struct avl_node *node) |
| static struct avl_node * | avl_local_min (struct avl_node *node) |
Function Documentation
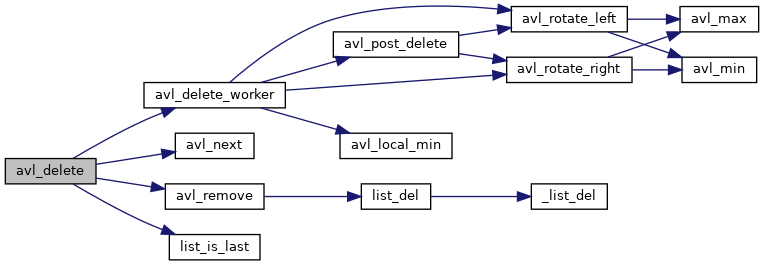
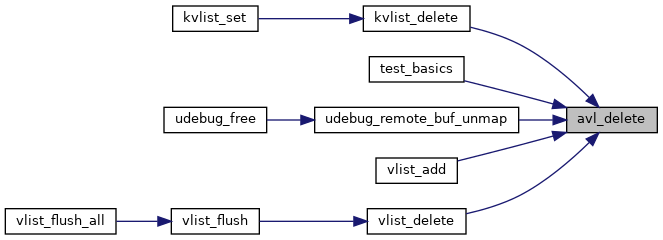
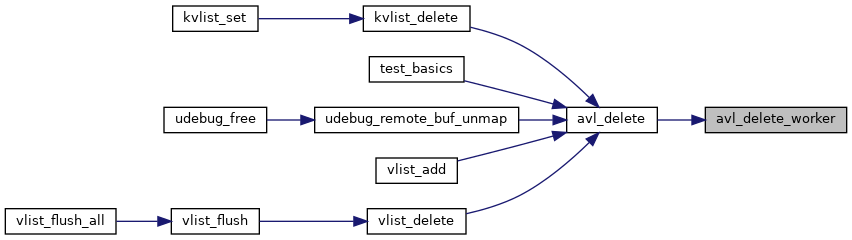
◆ avl_delete()
Remove a node from an avl tree
- Parameters
-
tree pointer to tree node pointer to node
Definition at line 307 of file avl.c.
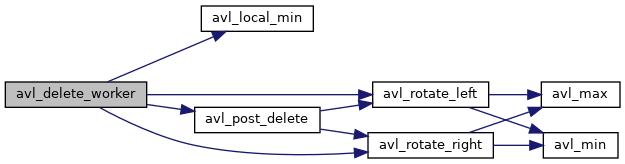
◆ avl_delete_worker()
Definition at line 594 of file avl.c.
◆ avl_find()
Finds a node in an avl-tree with a certain key
- Parameters
-
tree pointer to avl-tree key pointer to key
- Returns
- pointer to avl-node with key, NULL if no node with this key exists.
Definition at line 115 of file avl.c.


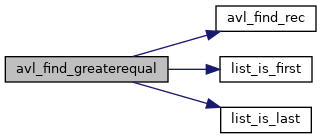
◆ avl_find_greaterequal()
Finds the first node in an avl-tree with a key greater or equal than the specified key
- Parameters
-
tree pointer to avl-tree key pointer to specified key
- Returns
- pointer to avl-node, NULL if no node with key greater or equal specified key exists.
Definition at line 179 of file avl.c.
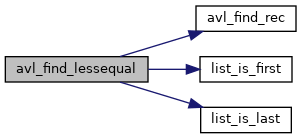
◆ avl_find_lessequal()
Finds the last node in an avl-tree with a key less or equal than the specified key
- Parameters
-
tree pointer to avl-tree key pointer to specified key
- Returns
- pointer to avl-node, NULL if no node with key less or equal specified key exists.
Definition at line 137 of file avl.c.
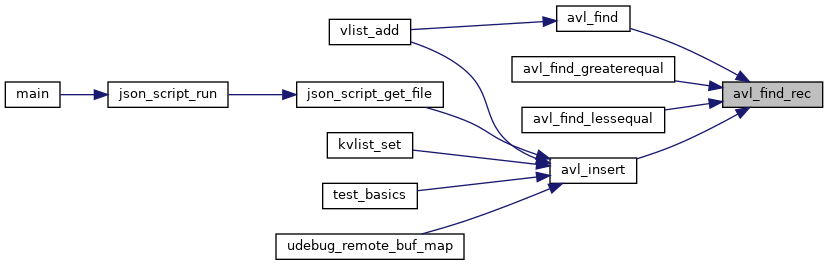
◆ avl_find_rec()
|
static |
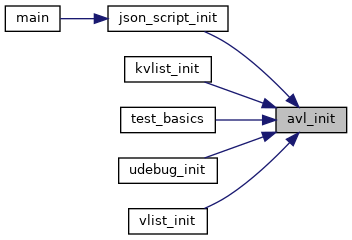
◆ avl_init()
| void avl_init | ( | struct avl_tree * | tree, |
| avl_tree_comp | comp, | ||
| bool | allow_dups, | ||
| void * | ptr | ||
| ) |
Initialize a new avl_tree struct
- Parameters
-
tree pointer to avl-tree comp pointer to comparator for the tree allow_dups true if the tree allows multiple elements with the same ptr custom parameter for comparator
Definition at line 92 of file avl.c.

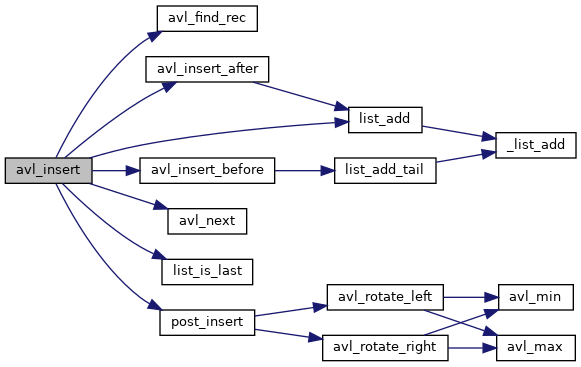
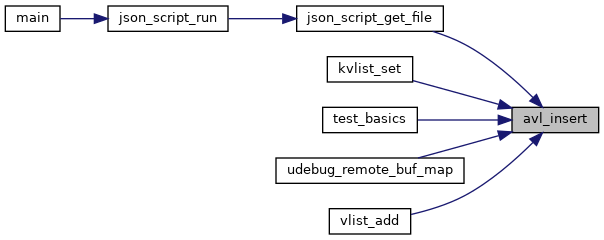
◆ avl_insert()
Inserts an avl_node into a tree
- Parameters
-
tree pointer to tree new pointer to node
- Returns
- 0 if node was inserted successfully, -1 if it was not inserted because of a key collision
Definition at line 220 of file avl.c.
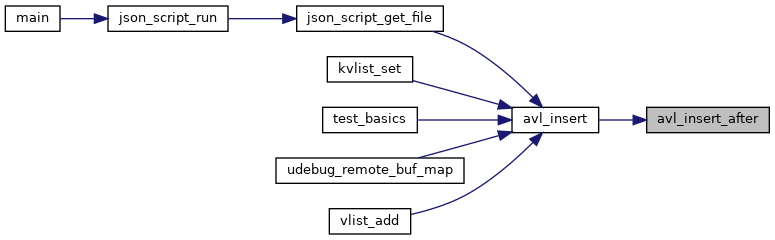
◆ avl_insert_after()
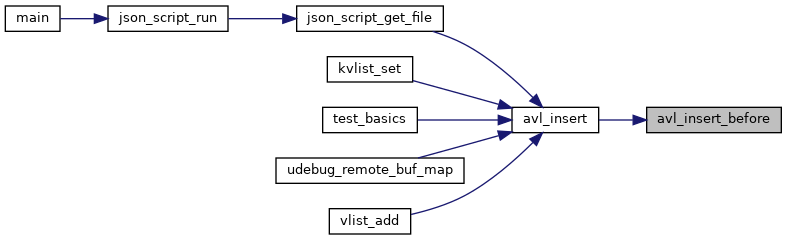
◆ avl_insert_before()
|
static |
Definition at line 491 of file avl.c.

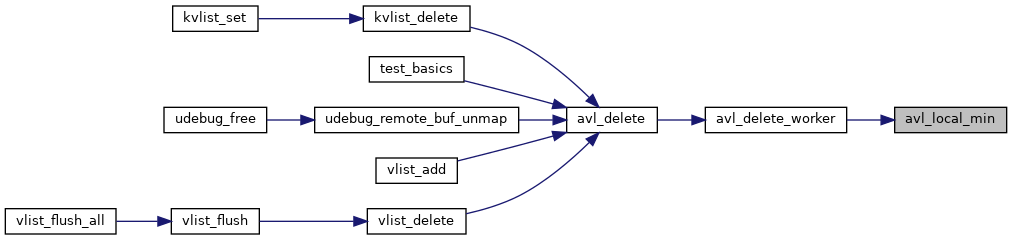
◆ avl_local_min()
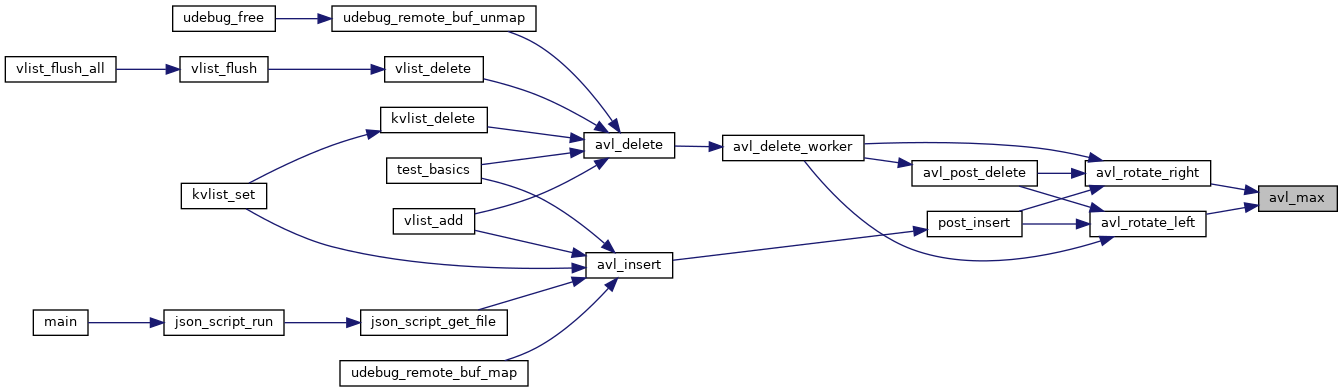
◆ avl_max()
|
inlinestatic |
internal type save inline function to calculate the maximum of to integers without macro implementation.
- Parameters
-
x first parameter of maximum function y second parameter of maximum function
- Returns
- largest integer of both parameters
Definition at line 59 of file avl.c.
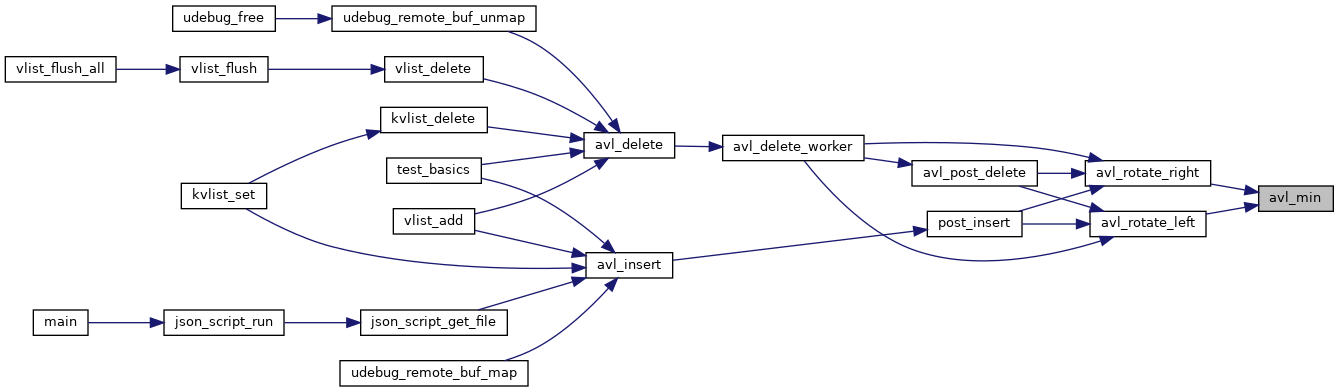
◆ avl_min()
|
inlinestatic |
internal type save inline function to calculate the minimum of to integers without macro implementation.
- Parameters
-
x first parameter of minimum function y second parameter of minimum function
- Returns
- smallest integer of both parameters
Definition at line 71 of file avl.c.